コイルに蓄積されたエネルギー
コイルにエネルギーが蓄積されるのでしょうか
コンデンサには電気エネルギーを貯めることができるのは電気の知識がある人にはわかることと思います。ところでコイル(インダクター)には電気エネルギーを貯めることができるのでしょうか。
もちろんコイルはコンデンサのように長い間 電気エネルギー楽天 を蓄積することはできません。純粋なコイルに電流を流すと、コイルは電気エネルギーを消費しませんから、その電気エネルギーはどこへ行ったのでしょうか。そうです、コイルに蓄積されているのです。
コイルに一時的に貯めたエネルギーの計算
コイルに直流電圧を掛けた時の電流
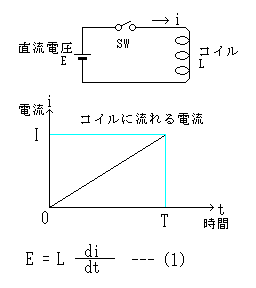
コイルに直流電圧を掛けた時の電流は左の図のようになります。(1)式のように直流電圧を E [V]、コイルのインダクタンスを L [H] とすると、レンツの法則により di/dt は一定の値となります。
時間0でスイッチを入れると、コイルの電流は増加率が一定で時間と共に増加します。つまり T [秒]後の電流は I [A] となります。もちろん、コイルの抵抗がゼロで電源が理想の定電圧源なら時間が経てば電流は無限大まで増大します。
普通のコイルは抵抗があるし、普通の電源には内部抵抗がありますから、コイルの電流は頭打ちになります。
(1)式の di/dt は I/T と等しいので
E = LI/T または I = ET/L となります。
この式はコイルにノコギリ波を流す場合に使われます。ブラウン管式のテレビの水平偏向電流の計算に使いました。
コイルに蓄積されたエネルギーの計算
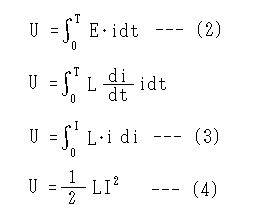
流れた電気エネルギーはどこにも消費されないので、このエネルギー U [J] がコイルに蓄積されたエネルギーとなります。これは(2)式のように瞬間の電力を時間で積分したものになります。
(2)式に(1)式を代入して計算すると、(3)、(4)式のようになります。
つまりコイルに蓄積されるエネルギーUは
U = L I 2/ 2
となります。ここで、Lが一定ならコイルに蓄積されたエネルギーはその時点に流れていた電流の2乗に比例するということです。
コイルにエネルギーを多く蓄積する方法と問題点
コイルに蓄積されるエネルギーを増やす為には、(4)式から考えてコイルのインダクタンスを大きくするか、コイルの電流を増やすかのどちらかです。
一般の磁性体入りコイルに電流を流して、この電流を増やしていくと磁性体が磁気飽和を起こしてきます。そうするとコイルのインダクタンスの値(L値)が小さくなってきます。その為、コイルに蓄積されるエネルギーが頭打ちになります。また磁気飽和を起こさないようにコアにギャップを設ける場合がありますが、こうするとインダクタンスが小さくなってしまいます。
コイルに蓄積されるエネルギーを増やすには必然的に磁性体を大きくするしかないのが実情です。
コイルに蓄積されたエネルギーの応用
コイルにエネルギーが蓄積されると何の役に立つのでしょうか。
- コイルとコンデンサを接続してコイルのエネルギーとコンデンサのエネルギーをやり取りさせると共振現象が起こります。これが直列共振や並列共振として利用されます。
- コイルに流れている電流を突然切ると、そのコイルに蓄積されたエネルギーは行き場を失ってしまいます。レンツの法則によってコイルに高電圧が発生します。これは自動車のエンジンの点火装置や電気柵の電撃装置等に利用されています。
- 同様にコイルの電流を入り切りしてコイルとコイルを鉄心等で結合させれば、トランスを作ることができます。スイッチングレギュレーターで電圧の上げ下げに使われています。
- 色々な研究機関で超伝導コイルに電力を貯蔵する方法をまじめに研究しているようです。非常に難しいことですが、もし実現できれば動く部分が無くて応答が速いので画期的なことです。SMES (Superconducting Magnetic Energy Storage)というようです。
- その他にもコイルを利用した物は何らかの形でコイルに蓄積されたエネルギーを利用しています。
