接地抵抗の計算と接地抵抗の概念

実際の接地抵抗(アース抵抗)は簡単に計算できるものではありませんが、接地抵抗とはどういう性質があるのかを見極める為に、土壌が均一なものとして積分によって接地抵抗を計算により求めてみました。接地抵抗を小さくする方法についても述べています。

接地抵抗の計算

接地抵抗楽天 とは、アース電極(接地電極)から地球の深部までの抵抗の事です。土壌の抵抗率から接地抵抗を計算により求め、接地抵抗とはどのような性質のものなのかを見てみます。土壌の抵抗率は　約10~1000[Ω・m]　で、普通の土壌では 約100[Ω・m] です。

接地電流の大地への拡散

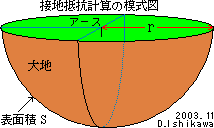　この接地抵抗計算の模式図で、半球の中央に接地が施してあり、半球の上の面を地表面とします。

土壌の電気的性質がどこでも均一なものと仮定すると、中央のアースから流れた電流は四方八方の大地に拡散して、半球上の点はどこでも等しい電流が流れていると考えられます。この為、半球上の点は全て電位が等しくなっていると考えられます。電位の等しい点同士は導線で結んでも電気的には何の影響もありません。従ってこの半球の表面は薄い導体と考えてもかまいません。

この半球の半径を r [m] とするとその表面積 S [m²] は球の半分で

S = 2π r²　となります。

積分による接地抵抗の計算

この半球の表面に微小厚さ Δr の土が付いているものとしてこの厚さ Δr の土だけの抵抗値 ΔR [Ω]　は、土の抵抗率を ρ [Ω・m]　とすると、

ΔR = ρ・Δr / S

つまり式1のようになります。接地抵抗はこの式1をある範囲から無限大まで加えたものとなります。すなわち式1を積分すれば良いことになります。

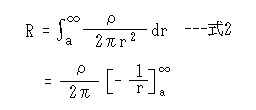
この半球に付いた微小厚さの土の抵抗を半径が無限小から無限大まで積分すると、接地抵抗は無限大になってしまいます。

この為、この半球の半径を有限の a [m] から無限大まで積分することにしました。つまり接地極を半径 a [m] の半球形状とした時の接地抵抗 R を式2のように計算できることになります。

この結果は

R = ρ/(2πa)　　　- - -式3　　　　のようになります。

半球形状の接地極の接地抵抗の計算結果

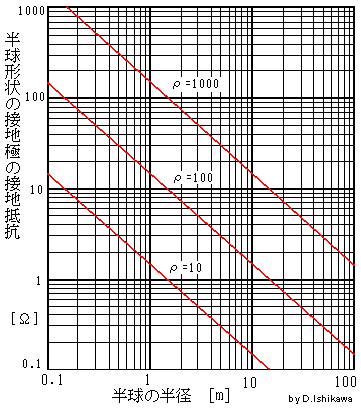　このグラフは式3で半球形状の接地極の接地抵抗を計算したものです。

このグラフからρ=100[Ω・m]以下では、半球の半径5m~10m以上の抵抗値は1.6Ω~3Ω以下となり無視しても問題ないレベルです。つまり接地抵抗は半径5~10m以内の状態で決まってしまうということです。(ρ=1000[Ω・m]では半径50~100m以上)

接地電極(アース電極)はできるだけ大きくするか、接地電極の周辺を電気を通し易い材質にすると接地抵抗を下げる事が可能です。

つまり接地抵抗は半径約10m以内の半球内の土の抵抗率と接地極の大きさに大きく依存するということです。

必要な接地抵抗の値にする為の接地極の大きさを上のグラフから推定することができます。例えば100Ω以下の接地抵抗を得る為には、ρ=1000 [Ω・m] では半径1.5mの半球と同等以上のものを接地極にすれば良いことがわかります。つまり直径3m以上の範囲に長さ1.5m以上のアース棒を何本か打ち込めば良いことがわかります。

接地抵抗を小さくする方法

• アース(接地)の電極はできるだけ大きくします。
• アース(接地)の電極はできるだけ深く埋めます。
• アース(接地)の電極から10メートル以上離れた場所にアース(接地)を複数個設置して、これらを相互に並列に接続します。
• アース(接地)電極付近の土壌に電気を通し易い炭や食塩や接地抵抗低減剤　(商品名　アスロン、サンアース、ドーデンクリート、チコーゲル、アモルアース、ニッピアース　等)　を混ぜて土壌の抵抗率を下げます。
• これらの方法を組み合わせて行なえば更に接地抵抗を小さくすることができます。

簡単に要約すると、接地抵抗を小さくするには、アース電極はできるだけ大きく、できるだけ深く、できるだけ広い範囲に、できるだけ電気を通しやすいように設置することが重要なのがわかります。