電気柵の静電容量の計算と考察
電気柵を設置する時に柵と大地アース間の電気抵抗つまり漏電が問題になる場合が多いのですが、電気柵と大地アース間の静電容量(コンデンサ成分)も無視できません。これが電気柵にどの程度影響するのか、理論と実際で考察してみました。

漏電楽天 は電気柵のエネルギーが減ってしまって電気柵の効果が少なくなります。静電容量の影響は電気柵のエネルギーが減る訳ではありせんが、ピークの高圧値が下がる原因になります。
この静電容量が電気柵システムにどの程度影響するのか、理論と実際で考察してみました。
水平に張った電線と大地アース間の静電容量の計算
水平に張った電線付近の電界分布
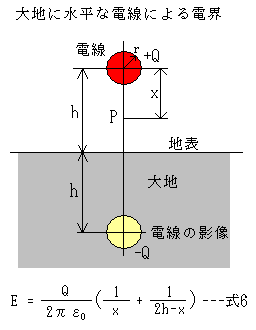
左の図は水平に張られた電線による電界を表わした模式図です。
ここで電線の半径をrとし、電線と大地の距離をh、電線の電荷を+Qとし、地面から下へh離れた電線の影像の電荷を-Qとします。
このように影像法では、大地から上の電界の分布は、大地が無くて地面から下へh離れた電線の影像の電荷を-Qとした時と全く同じと考えられます。
そうすると、
電線による電界=Q/2πε0x
電線の影像による電界=-Q/2πε0(2h-x)
電界の向きを考えて加えると、電線から下方向にxだけ離れた点Pの電位Eは式6のようになります。
水平に張った電線の電圧計算(積分)
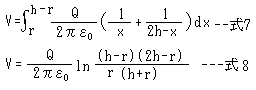
式7は電線と大地アース間の電圧を計算したもので、式6の電位をrからh-rまで積分して求めることができます。その結果は式8のようになります。ln は自然対数です。
水平に張った電線の静電容量の計算
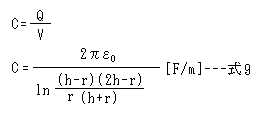
C = Q/V だから、式8から電線と大地アース間の1m当たりの静電容量Cは式9のように計算できます。MKS単位系です。
この式はどこかの本に載っていてもよいと思ったのですが、私が探した限りでは見つけることができませんでした。仕方なく自分で積分して導きました。
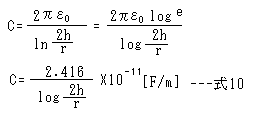
ここで h >> r とすると、電線と大地アース間の1m当たりの静電容量は式9を変形して左のようになります。log は常用対数です。
真空中の誘電率 ε0 ≒ 8.854 X 10-12
e≒2.718 log e ≒ 0.4343
電線と大地アース間の1m当たりの静電容量は式10のように計算できます。
水平に張った電線の静電容量の計算結果
| 電線の高さh[m] | 0.02 | 0.05 | 0.1 | 0.2 | 0.5 | 1 | 2 | 5 | 10 | 20 | 50 | 100 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 静電容量[PF/km] | 12,700 | 10,500 | 9,280 | 8,320 | 7,320 | 6,710 | 6,190 | 5,620 | 5,250 | 4,930 | 4,560 | 4,310 |
電線の太さは半径0.5mm(直径1mm)
| 電線の半径r[mm] | 0.05 | 0.1 | 0.2 | 0.5 | 1 | 2 | 5 |
|---|---|---|---|---|---|---|---|
| 静電容量[PF/km] | 6,190 | 6,710 | 7,320 | 8,320 | 9,280 | 10,500 | 12,700 |
電線の高さは20cm一定
水平に張った電線の電気柵の静電容量の考察
- 電線を水平に1本張る場合はその高さが少々変化しても静電容量にはあまり影響しません。すなわち電線と大地の間の電気力線が静電容量に影響して電線より上の電気力線は静電容量にあまり影響が無いということです。
- 電線の太さによっても電線とアース間の静電容量にはあまり影響しません。
- ということは電線を上下に2本張っても何本張っても並列にして同じ電圧を掛けるのなら柵の電線の静電容量は1本の時より少し増加するだけと推定されます。
- 一般的な電気柵の静電容量は柵の長さ100m当たり1,000PF程度ということが解りました。(電線の長さではありません。柵の長さです。)
- 電気柵の静電容量は想像していたより多かったというのが私の実感です。
柵の長さ約500mの電気柵での実験結果
実際に柵の長さ500m程度の電気柵(柵の電線の高さ約25cm,60cmの2段、一部高さ90cmを加えた3段)を設置して電気柵とアース間の容量の影響を調べてみましたら約5,000PFの静電容量と同等の動作波形となりました。
LCRブリッジ(リーダーのLCR-740)でも測定してみました。その結果は5,500PFと270kΩの並列回路とほぼ同等の測定値でした。
静電容量の測定値が計算値よりも少し多めなのは、草の影響や地面の起伏の影響があり、また一部で電気柵とトタンの柵の両方を使用している部分があり、実際は電線がもっと地面に近い所にあるのと同等になっているものと思われます。270kΩの抵抗値は草や支柱の漏電です。この電気柵は管理が良く絶縁は良い方です。
二本の電線間の静電容量の計算
猿やハクビシン対策で電気柵の電線の高圧とアースの線を交互に上下に並べて配置する方法があります。この場合の電気柵の静電容量を計算してみました。
2本の電線間の電界分布
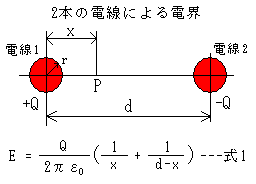
左の図は2本の平行に張られた電線による電界を表わした模式図です。
ここで電線の半径をrとし、電線1と電線2は距離dで平行に張られているものとします。電線1の電荷を+Qとし、電線2の電荷を-Qとします。
そうすると、
電線1による電界=Q/2πε0x
電線2による電界=-Q/2πε0(d-x)
電界の向きを考えて加えると、電線1から電線2方向にxだけ離れた点Pの電位Eは式1のようになります。
2本の電線間の電圧計算(積分)
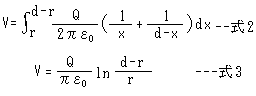
式2は2本の電線間の電圧を計算したもので、式1の電位をrからd-rまで積分して求めることができます。その結果は式3のようになります。ln は自然対数です。
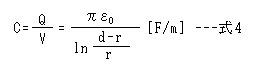
C = Q/V だから、式3から2本の電線間の1m当たりの静電容量Cは式4のように計算できます。MKS単位系です。
2本の電線間の静電容量の計算
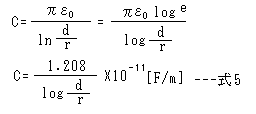
ここで d >> r とすると、2本の電線間の1m当たりの静電容量は式4を変形して左のようになります。log は常用対数です。
真空中の誘電率 ε0 ≒ 8.854 X 10-12
e≒2.718 log e ≒ 0.4343
2本の電線間の1m当たりの静電容量は式5のように計算できます。この式は高圧送電線の電線間の静電容量の計算に使われています。
2本の電線間の静電容量の計算結果
| 電線間の距離[m] | 0.01 | 0.02 | 0.05 | 0.1 | 0.2 | 0.3 | 0.5 | 1 | 2 | 5 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 静電容量[PF/km] | 9,280 | 7,540 | 6,040 | 5,250 | 4,640 | 4,350 | 4,030 | 3,660 | 3,350 | 3,20 | 2,810 |
電線の太さは半径0.5mm(直径1mm)
猿やハクビシン用電気柵の電線間の静電容量の考察
- 電気柵の電線を高圧とアース電位を交互に設置する場合は柵の静電容量を計算する時、柵の長さだけでなく電線の長さを考慮しなければならない。
- 一番下の高圧の電線は大地との間の静電容量の計算式で計算します。(10,000PF/km)
- それより上の電線の静電容量は電線間の静電容量の計算式で計算します。(4,500PF/km)
- 例として5段の電気柵を猿用に300メートル設置した場合は(10,000+4,500X4)X0.3=8,400PF となり1kmの普通の電気柵とほぼ同じ静電容量となり柵をあまり長くできないことが解ります。